Open Access, Peer-reviewed
eISSN 2093-9752
Open Access, Peer-reviewed
eISSN 2093-9752
Young-Seong Lee
Soo-ji Han
http://dx.doi.org/10.5103/KJAB.2025.35.3.131 Epub 2025 August 01
Abstract
Objective: This study aimed to investigate how running speed influences impact characteristics across the human body by analyzing vertical ground reaction force, time-domain impact acceleration, and frequency-domain components. The focus was on quantifying changes in both impact and active force, segmental acceleration amplitudes, and high-frequency impact behavior.
Method: Seventeen healthy recreational runners (age: 26.65 ± 4.73 years, height: 177.05 ± 3.46 cm, weight: 72.06 ± 10.13 kg) performed treadmill running at four different speeds (2.5, 3.0, 3.5, and 4.0 m/s). Vertical ground reaction force was collected and separated into impact and active components using low- and high-pass filtering at a 10 Hz cutoff. Tri-axial accelerometers were attached to five body segments (distal tibia, proximal tibia, L5, sternum, and head). Time-domain acceleration peaks were extracted in vertical, horizontal, and resultant directions. Frequency-domain analysis was conducted using the Welch method to compute peak frequency and power spectral density (PSD) within the 10-20 Hz band. Two-way repeated measures ANOVA was used to assess the effects of speed and body segment.
Results: As running speed increased, both impact and active force significantly increased (p<.05). Time-domain acceleration magnitudes also rose significantly across all segments, with the distal and proximal tibia showing the largest increases. In the frequency domain, PSD values increased markedly with speed, especially in the lower limbs, while peak frequency remained relatively stable (13-16 Hz) without significant change. Notably, the proximal tibia exhibited consistently higher PSD values than the distal tibia in the high-frequency range. Vertical acceleration consistently showed the highest amplitude and PSD across all axes.
Conclusion: This study demonstrates that increased running speed amplifies mechanical loading as reflected in ground reaction forces, segmental accelerations, and high-frequency impact content. The results highlight the role of the lower extremities, particularly the proximal tibia, in absorbing and potentially accumulating high-frequency vibrations. The observed discrepancy between time- and frequency-domain findings suggests complex transmission and damping behavior influenced by anatomical and tissue properties. These findings have implications for injury prevention, training strategies, and footwear design by emphasizing the need for targeted shock attenuation, especially during high-speed running.
Keywords
Running speed Body impact Shock acceleration Frequency analysis
전 세계적으로 달리기에 참여하는 인구는 꾸준히 증가하고 있으며, 이에 따라 달리기 관련 부상(running-related injury, RRI)의 발생률 또한 높은 수준으로 보고되고 있다. 기존 연구에 따르면, 러너 집단의 연간 RRI 발생률은 연구 설계와 대상자 특성에 따라 약 11%에서 92%까지 다양하게 나타나며, 일부 문헌에서는 전체 러너의 최대 85%가 RRI를 경험한다고 보고되고 있다(Malisoux et al., 2021; Nielsen, Buist, Sørensen, Lind & Rasmussen, 2012; Van Gent et al., 2007). RRI는 다양한 원인에 의해 발생할 수 있으나(Malisoux, Nielsen, Urhausen & Theisen, 2015), 다수의 연구에서는 지속적이고 반복적인 충격(impact)을 주요 기전으로 지목하고 있다. 반복되는 충격의 누적은 경골 피로골절(tibia stress fracture), 무릎 통증, 족저근막염 등과 같은 대표적인 과사용 부상(overuse injury)을 유발하는 주요 기전으로 알려져 있으며(Hreljac, Marshall & Hume, 2000; Malisoux et al., 2021), 주간 주행 거리의 급격한 증가, 고강도 훈련의 급증, 회복 시간 부족, 갑작스러운 지면 변화와 같은 훈련 오류(training errors)로 인해 신체 조직이 이러한 충격에 적응할 시간이 부족할 경우 RRI 위험률은 더욱 증가할 수 있다(Malisoux et al., 2021; Nielsen et al., 2012).
충격은 특정 주파수 영역(frequency domain)에서 발생하며, 이를 통해 신체에 미치는 충격의 크기와 빈도를 정량적으로 평가할 수 있다. 따라서, 주파수 기반의 충격 분석은 단순한 크기 비교를 넘어 충격의 질적 특성을 이해하는 데 필수적이다(Gruber, Boyer, Derrick & Hamill, 2014; Malisoux et al., 2021; Shorten & Winslow, 1992; Winslow & Shorten, 1989). 달리기 시, 인체는 저주파(low-frequency: 3-8 Hz)와 고주파 성분(high-frequency: 9-20 Hz)의 진동을 받는다. 저주파는 주로 몸통과 하지 전체 움직임을 유발하는 근육과 관절의 능동적 감쇠(active attenuation)로 발생되는 반면, 고주파는 초기 지면 접촉 시, 발이나 경골의 급격한 감속에 나타나며, 이는 근육 반응 시간보다 빨라 수동적 감쇠(passive attenuation)에 의존하게 된다(Gruber et al., 2014; Shorten & Winslow, 1992; Winslow & Shorten, 1989). Shorten과 Winslow (1992)는 10-20 Hz의 고주파 충격이 신체 내에서 효과적으로 감쇠되지 않아 조직에 상당한 부담을 줄 수 있으며, 특히 15 Hz 이상의 주파수 대역이 부상 위험이 높은 주파수 영역(high-risk frequency band)으로 제안하였다. 이처럼 특정 주파수 성분의 분석을 통해 인체 각 부위에 미치는 충격의 영향을 명확하게 파악할 수 있으며, 이를 통해 RRI 예방에 크게 기여할 수 있다. 그러나 기존의 RRI 연구 대부분은 시간 영역(time domain) 분석에 국한되어 있으며(Gruber et al., 2014; Shorten & Winslow, 1992), 이 접근은 충격 분석 결과가 가속도계의 부착 위치, 중력, 하지의 각속도 등 외부 요인의 영향을 크게 받아 실제 충격의 크기를 과소 혹은 과대평가할 수 있다는 한계를 가진다(Lucas-Cuevas, Encarnación-Martínez, Camacho-García, Llana-Belloch & Pérez-Soriano, 2017). 또한 Gruber 등 (2014)는 충격 전달(transmissibility)이 주파수 성분에 의해 결정된다고 보고하였으며, 주파수 영역(frequency domain) 분석 없이는 감쇠 메커니즘을 명확히 이해하기 어렵다고 강조하였다. 달리기 시, 신체 내 충격 주파수(impact frequency)는 조직 별 감쇠 능력과 밀접하게 관련되어 있으며, 감쇠 메커니즘 자체가 주파수에 의존적일 수 있다. 따라서 충격으로 인한 상해 위험성을 명확히 규명하기 위해서는 시간 영역 분석을 보완할 수 있는 주파수 기반 분석이 필수적으로 요구된다(Gruber et al., 2014; Malisoux et al., 2021; Shorten & Mientjes, 2011).
달리기 시, 신체에 가해지는 충격은 달리기 속도에 따라 변화된다. 일반적으로 속도가 증가하면 지면과의 접촉 시간은 짧아지고, 발 착지 시 발생하는 지면반력(ground reaction force)은 더욱 커지게 된다(Kyröläinen, Komi & Belli, 1999; Hollis, Koldenhoven, Resch & Hertel, 2019). 이러한 역학적 변화는 하지 분절에 전달되는 충격의 강도를 증가시켜 반복적인 노출 시, 조직 손상의 위험을 높일 수 있다(Hamill, Derrick & Holt, 1995; Shorten & Winslow, 1992). 기존의 선행연구를 살펴보면, 속도가 증가할수록 경골이나 발 뒤꿈치에서 측정된 충격 가속도(impact acceleration)와 충격의 전파(transmission)가 유의하게 증가되며(Gruber et al., 2014; Ryu, Yoon & Park, 2016), 특히 착지 직후의 하지 분절 감속 속도는 속도 증가에 민감하게 반응하고 빠른 달리기에서의 급격한 가속도 변화가 더욱 뚜렷하게 나타난다(Gruber et al., 2014).
이와 같은 역학적 변화는 단순한 기계적 부하의 증가를 의미할 뿐만 아니라, 신체 조직이 감내해야 하는 물리적 스트레스의 강도와 주파수 성분의 변화를 야기할 수 있다는 점에서 중요한 의미를 가진다. 특히, 빠른 속도의 달리기에서는 고주파 대역(>15 Hz) 노출이 상대적으로 증가할 수 있으며, 이는 곧 RRI의 위험 증가와 직결될 수 있다(Shorten & Winslow, 1992). 그러나, 속도 변화가 충격의 물리적 특성에 미치는 영향은 대부분 시간 영역 분석에 국한되어 왔으며, 충격 가속도의 최대 크기와 같은 단순 지표로 해석되는 경우가 많았다. 이를 보완하고자 본 연구는 충격 주파수 영역대인 10-20 Hz에서의 고주파 영역 파워 스펙트럼 밀도(power spectral density, PSD)와 최대 주파수(maximum frequency)를 분석하여, 고주파 에너지의 분포와 증폭 특성 등 충격의 질적 변화를 정량적으로 규명하고자 하였다. 이에 따라, 본 연구는 달리기 속도 변화가 신체 각 분절에 전달되는 충격의 주파수 성분에 어떤 영향을 미치는지를 분석하였다.
따라서, 본 연구의 목적은 달리기 속도에 따라 인체 주요 분절(먼쪽 정강뼈, 몸쪽 정강뼈, 5번째 허리뼈, 가슴뼈, 머리)에서 측정된 충격 가속도의 주파수 성분이 어떻게 변화하는지를 규명하는 것이다. 이를 통해 각 부위 별로 고주파 노출 위험이 달라지는지를 분석하고, RRI와의 관련성을 파악할 수 있는 기초자료를 제공하고자 한다. 본 연구의 목적을 통해 다음과 같은 가설을 설정하였다. 첫째, 달리기 속도가 증가할수록 인체 각 분절에서 측정되는 충격 가속도의 고주파 성분 비율은 유의미하게 증가할 것이다. 둘째, 달리기 속도 증가에 따른 주파수 성분의 변화는 신체 분절 별 상이하게 나타나며, 특히 하지 부위(먼쪽 정강뼈, 몸쪽 정강뼈)에 고주파 성분이 집중될 것이다.
1. 연구 대상자
본 연구는 건강한 젊은 레크레이션 러너 17명(연령: 26.65±4.73 years, 신장: 177.05±3.46 cm, 체중: 72.06±10.13 kg)을 대상으로 달리기 속도에 따른 신체 분절에서의 충격을 분석하였다. 연구 대상자는 주 2회 이상 후족 착지 달리기를 하며, 6개월 내 하지의 근골격계 상해가 없고 신발 사이즈가 265 mm인 대상자를 조건으로 모집하였다. 총 25명의 대상자가 모집되었으며, 이 중 속도에 따라 착지 유형이 달라지거나 독특한 달리기 동작 또는 부착 오류에 따라 자료에 이상치가 발생한 대상자는 모두 제외하였다. 본 연구는 K대학교의 생명윤리위원회의 연구윤리 승인(1263-202205-HR-028-01)을 받아 진행하였으며, 모든 연구 대상자들의 동의를 받아 진행하였다.
2. 실험 절차
본 연구를 수행하기 위해 8대의 적외선 카메라(Oqus, Qualisys, Sweden; sf: 100 Hz)와 지면반력이 내장된 트레드밀(Instrumented treadmill, Bertec, USA; sf: 1,000 Hz), 3축 가속도계 5채널(Ultium, Noraxon, USA; sf: 1,000 Hz)을 사용하였다. 달리기 시, 신체가 받는 충격은 착지 유형에 따라 충격의 특성이 달라지므로(Almeida, Davis & Lopes, 2015; Lieberman et al., 2010; Lopes, Hespanhol, Yeung & Costa, 2012), 지면과 발 사이의 각도를 통해 각 속도에서의 착지 유형을 확인하였다. 후족 착지 시, 지면과 발 사이의 각도는 선행연구에 따라 14.8-29.1°로 설정하였다(Arendse et al., 2004; Breine et al., 2017; Kulmala, Avela, Pasanen & Parkkari, 2013a). 모든 연구 대상자는 준비운동 및 트레드밀 적응을 위해 걷기부터 달리기까지 약 5분 동안 수행하였으며, 이 후 실험복으로 환복하고 반사마커(reflective marker) 및 가속도계를 부착하였다. 반사마커는 오른쪽 2번째 발허리뼈(2nd metatarsal bone)와 발 뒤꿈치(heel), 바깥쪽 발목(lateral ankle), 바깥쪽 무릎(lateral knee)에 부착하였으며, 가속도계는 먼쪽 정강뼈와 몸쪽 정강뼈(Glauberman & Cavanagh, 2014; Ryu, Lee & Park, 2021), 5번째 허리뼈(Castillo & Lieberman, 2018), 앞 가슴뼈(Reenalda, Maartens, Buurke & Gruber, 2019), 머리(Hamill et al., 1995; Mercer, Bates, Dufek & Hreljac, 2003)에 각각 양면 테잎으로 1차 부착 후, 탄력밴드(elastic band)로 단단히 감아 고정시켰다(Park et al., 2022; Ryu et al., 2021). 먼쪽 정강뼈(distal tibia)는 오른쪽 발목 안쪽 복숭아뼈(medial malleolus)로부터 약 5 cm 위에 부착하였으며, 몸쪽 정강뼈(proximal tibia)는 오른쪽 무릎 아래 정강뼈 거친면(tibia tuberosity)에 부착하였다. 가속도의 축 방향은 먼쪽 정강뼈에서 몸쪽 정강뼈를 잇는 수직 방향을 +z축(vertical axis)로 설정하였으며, z축과 직각을 이루는 축을 전-후축(anteriorposterior axis) 및 좌-우 축(medial-lateral axis)으로 설정하였다. 또한, 달리기 시, 신발에 따른 효과를 최소화하기 위해 모든 대상자는 동일한 신발(Air Zoom Pegasus 39, Nike, USA)을 착용하였다. 모든 달리기 준비를 마친 대상자는 무작위로 달리기 속도(2.5 m/s, 3.0 m/s, 3.5 m/s, 4.0 m/s)를 선정하여 각각 3분간 달리기를 수행하였으며, 각 속도에 따른 달리기 사이에는 충분한 휴식을 주었다. 달리기 3분 중 마지막 1분만을 녹화하였으며, 녹화 시작 오른발 첫 착지로부터 20 스텝(step)을 추출하여 분석하였다.
3. 자료 처리
본 연구는 달리기 속도에 따른 인체 충격 특성을 파악하기 위해, 인체가 지면에 가한 수직 지면반력(vertical ground reaction force)과 신체 각 분절의 충격 가속도를 측정하였다. 지면반력 자료는 QTM (Qualisys Track Manager)을 통해, 충격 가속도 자료는 MR3 (Noraxon, USA)를 통해 수집하였으며, 두 신호는 정확한 시점 비교가 가능하도록 동기화(synchro- nization)하였다. 대상자의 분석 구간은 오른발의 착지(foot contact) 시점부터 이지(toe-off) 시점까지로 정의하였으며, 수직 지면반력 값이 20 N이 되는 순간을 착지 및 이지 시점의 임계값(threshold)로 설정하여 총 20 스텝을 선별하였다. 획득된 모든 자료는 고주파의 노이즈를 최소화하기 위해 2차 버터워스 저역통과 필터(2nd-order Butterworth low-pass filter)를 적용하였으며, 이 때, 차단 주파수(cut-off frequency)는 수직 지면반력과 가속도 모두 100 Hz로 설정하였다.
수직 지면반력 자료는 분석 간 비교를 위해 각 대상자의 체중으로 정규화(normalization)하였으며, 이 후, 10 Hz를 기준으로 저역통과 필터링과 고역통과 필터링을 수행하여 수동 성분(passive portion)과 능동 성분(active portion)을 분리하였다(Blackmore, Willy & Creaby, 2016; Ryu & Yoon, 2005; Shorten & Mientjes, 2011; Figure 1).
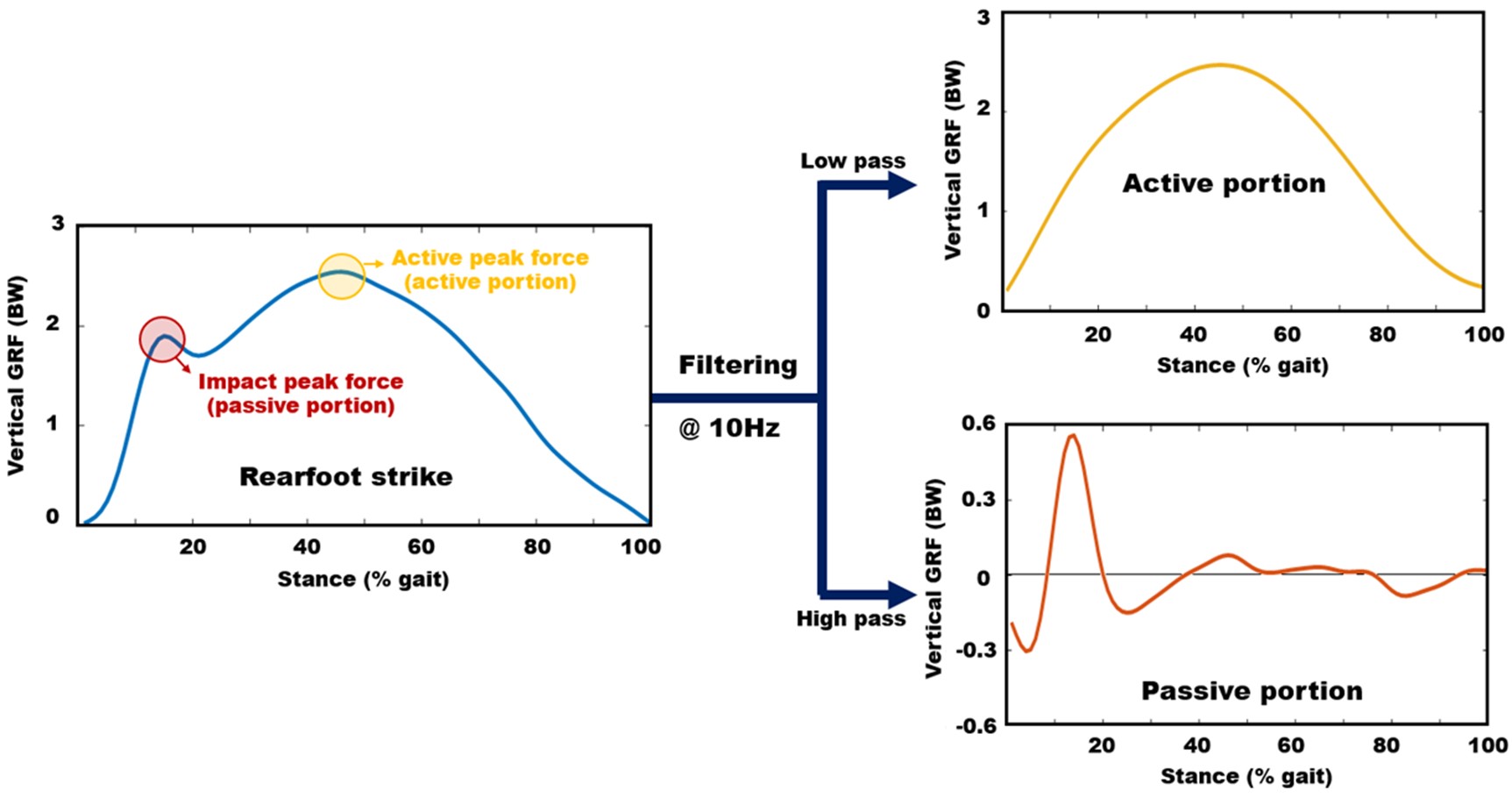
충격 가속도 자료는 시간 영역 분석과 함께 주파수 분석을 위해 전처리를 병행하였다. 시간 영역에서는 수직 성분과 수평 성분, 3축 합성 성분을 계산하여 성분 별 최대 가속도 값을 산출하였으며, 주파수 영역에서는 Welch 방법을 이용한 PSD 분석을 통해 충격 주파수 영역인 10-20 Hz 구간에서의 PSD와 최대 주파수를 추출하였다. Welch 방법은 충격 주파수의 최대 주파수를 안정적으로 추정할 수 있으며, 짧은 시간의 구간에서의 고주파 분석에 적합한 주파수 분석 방법이다(Figure 2; Same, Gandubert, Gleeton, Ivanov & Landry, 2020; Welch, 2003). 수직 지면반력 및 충격 가속도에 대한 모든 자료 처리는 MATLAB 2016a (The MathWorks, USA)를 통해 수행하였다.

4. 분석 변인
본 연구에서는 전처리된 수직 지면반력 및 충격 가속도 자료를 바탕으로, 속도 변화에 따른 인체 충격 특성을 정량적으로 비교하기 위해 다음과 같은 분석 변인을 산출하였다.
첫째, 수직 지면반력에서는 10 Hz로 필터링하여 추출한 수동 성분과 능동 성분의 최대값을 충격력(impact force)과 능동력(active force)으로 각각 정의하였다. 수직 지면반력은 착지 시 지면과의 충돌에 의해 발생하는 가장 직접적이며 신뢰도 높은 역학적 지표로, 인체가 지면에 가하는 중력 및 반작용력의 크기와 시점을 명확하게 반영한다(Ryu, 2020; Shorten & Mientjes, 2011). 그러나, 기존의 충격력 분석은 일부 러너에게서 명확한 피크 형태로 나타나지 않는다는 한계가 존재한다. 이에 따라 최근 연구에서는 수직 지면반력 신호를 충격 성분과 능동 성분으로 나누어 분석하는 접근법이 주목받고 있다. 두 값 모두 체중으로 정규화된 값을 사용하였다.
둘째, 충격 가속도는 다섯 개의 분절에 대해 분석하였으며, 각 분절의 수직 가속도, 수평 합성 가속도, 3축 합성 가속도를 계산하였다. 먼쪽 정강뼈에서의 수직 가속도는 수직 지면반력의 충격 변인인 최대 충격력 및 충격부하율과 매우 높은 상관관계(correlation[r]: 0.7-0.99)를 지니며(Hennig & Lafortune, 1991; Norris, Anderson & Kenny, 2014), 착지 유형에 따라 수직 및 수평 방향의 충격 특성이 다르게 나타나므로 충격 특성을 자세히 파악하기 위해서는 수평 합성 및 3축 합성 성분의 가속도를 고려해야 한다(Giandolini et al., 2016; Glauberman & Cavanagh, 2014; MacLellan & Vyvyan, 1981). 이에 시간 영역에서는 이들 세 성분 각각의 최대값(peak acceleration)을 분석에 사용하였다.
수평 합성 가속도=(x축 가속도)^2 + (y축 가속도)^2
3축 합성 가속도= (x축 가속도)^2 + (y축 가속도)^2 + (z축 가속도)^2
셋째, 주파수 영역에서는 각 가속도 신호를 스펙트럼으로 변환하여 수직, 수평 합성, 3축 합성 가속도에 대한 PSD와 최대 주파수를 추출하였다. PSD는 파워 스펙트럼 상 충격 주파수 영역인 10-20 Hz 내 최대 진폭 제곱값(g2/Hz)을 의미하며, 최대 주파수는 해당 파워가 발생한 주파수(Hz)를 의미한다.
5. 통계 분석
수직 지면반력과 충격 가속도의 특성은 기술통계를 통해 비교하였으며, 통계적 유의성과 함께 효과 크기(effect size)를 제시하였다. 또한, 충격 가속도 관련 변인은 95% 신뢰구간(95% confidence interval, CI)을 제시하였다. 속도에 따른 수직 지면반력의 충격 특성은 일원 반복측정 분산분석(one-way repeated measures ANOVA)을 통해 비교하였으며, 속도와 분절에 따른 인체의 충격 가속도 특성은 시간 영역 및 주파수 영역 모두 이원 반복측정 분산분석(two-way repeated measures ANOVA)을 통해 비교하였다. 비교를 통해 통계적으로 유의한 차이(α=.05)가 나타난 경우, Bonferroni 사후검정(post-hoc) 실시하였으며, 모든 통계 분석은 SPSS 21.0 (IBM, USA)으로 수행하였다.
1. 속도에 따른 수직 지면반력 특성 분석
달리기 속도가 증가함에 따라 최대 충격력와 최대 능동력는 유의하게 증가하였다(p<.05). 최대 충격력은 2.5 m/s에서 0.43±0.12 BW, 4.0 m/s에서 0.77±0.17 BW로 증가하였으며, 사후검정 결과 속도 간 유의한 차이가 나타났다. 최대 능동력 또한 속도가 증가함에 따라 증가하였으며, 유의한 차이를 보였다. 두 변수 모두 효과 크기는 η2 > .68로 매우 높게 나타났다(Table 1).
|
|
V1 |
V2 |
V3 |
V4 |
F (p) |
Post-hoc |
Effect size |
|
Impact peak |
0.43±0.12 |
0.49±0.13 |
0.64±0.17 |
0.77±0.17 |
35.32 (.001)* |
V1<V2<V3<V4 |
0.859 |
|
Active peak |
2.34±0.12 |
2.44±0.12 |
2.51±0.10 |
2.55±0.11 |
35.32 (.001)* |
V1<V2<V3,V4 |
0.688 |
|
Note. *: significant at p<.05;
V1: 2.5 m/s, V2: 3.0 m/s, V3: 3.5 m/s, V4: 4.0 m/s |
|||||||
2. 시간 영역에서의 충격 가속도: 속도 및 신체 분절에 따른 분석
시간 영역에서 측정된 수직, 수평 합성, 3축 합성 가속도는 속도와 신체 분절에 따라 유의한 차이를 보였다(p<.05). 속도 증가에 따라 세 축 모두에서 평균 가속도 값이 유의하게 증가하였으며, 특히, 4.0 m/s에서 가장 큰 값, 2.5 m/s에서 가장 작은 값이 나타났다. 신체 분절 간 비교에서는 유의한 주 효과가 나타났으며, 먼쪽 정강뼈에서 가장 큰 충격 가속도 값이, 머리에서 가장 낮은 충격 가속도 값이 나타났다. 속도와 신 체 분절에 따른 모든 충격 가속도에서 효과 크기(η2)는 .86-.92로 높게 나타났다(Table 2-3).
|
Axis |
Segment |
V1 |
V2 |
V3 |
V4 |
95% CI |
95% CI |
|
Vertical |
Distal tibia |
6.11±1.73 |
7.57±1.99 |
9.20±2.15 |
11.19±2.19 |
7.63 |
9.41 |
|
Proximal tibia |
5.47±0.99 |
6.07±0.82 |
7.58±1.59 |
8.98±1.51 |
6.49 |
7.55 |
|
|
L5 |
4.16±1.14 |
4.92±1.21 |
5.40±1.41 |
5.95±2.02 |
4.41 |
5.81 |
|
|
Sternum |
3.32±0.63 |
3.67±0.69 |
3.98±0.84 |
3.90±0.72 |
3.40 |
4.03 |
|
|
Head |
2.24±0.29 |
2.40±0.38 |
2.49±0.38 |
2.67±0.41 |
2.27 |
2.63 |
|
|
95% CI (lower) |
3.91 |
4.55 |
5.33 |
6.11 |
- |
- |
|
|
95% CI (upper) |
4.62 |
5.30 |
6.14 |
6.96 |
- |
- |
|
|
Horizontal Acc. |
Distal tibia |
5.67±1.40 |
7.00±2.10 |
8.17±2.78 |
10.28±2.84 |
6.765 |
8.78 |
|
Proximal tibia |
4.15±0.73 |
4.96±0.84 |
5.50±0.80 |
6.59±0.91 |
4.916 |
5.69 |
|
|
L5 |
2.01±0.53 |
2.19±0.55 |
2.48±0.50 |
3.05±0.78 |
2.160 |
2.70 |
|
|
Sternum |
1.44±0.42 |
1.53±0.40 |
1.67±0.53 |
1.76±0.53 |
1.408 |
1.80 |
|
|
Head |
1.20±0.32 |
1.22±0.44 |
1.30±0.35 |
1.22±0.37 |
1.059 |
1.41 |
|
|
95% CI (lower) |
2.69 |
3.12 |
3.53 |
4.26 |
- |
- |
|
|
95% CI (upper) |
3.10 |
3.64 |
4.12 |
4.90 |
- |
- |
|
|
3-axis |
Distal tibia |
7.65±1.61 |
9.42±1.88 |
11.39±2.27 |
14.16±2.39 |
7.63 |
9.41 |
|
Proximal tibia |
6.10±1.15 |
7.10±1.03 |
8.65±1.55 |
10.41±1.49 |
6.49 |
7.55 |
|
|
L5 |
4.48±1.11 |
5.16±1.21 |
5.69±1.34 |
6.32±1.94 |
4.41 |
5.81 |
|
|
Sternum |
3.55±0.67 |
3.94±0.62 |
4.25±0.85 |
4.23±0.69 |
3.40 |
4.03 |
|
|
Head |
2.53±0.26 |
2.69±0.31 |
2.79±0.28 |
2.90±0.31 |
2.27 |
2.63 |
|
|
95% CI (lower) |
3.91 |
4.55 |
5.330 |
6.11 |
- |
- |
|
|
95% CI (upper) |
4.62 |
5.30 |
6.14 |
6.96 |
- |
- |
|
|
Note. V1: 2.5 m/s, V2:
3.0 m/s, V3: 3.5 m/s, V4: 4.0 m/s; 95% CI: 95% confidence interval |
|||||||
|
Axis |
|
F (p) |
Post-hoc |
Effect size (η2) |
|
Vertical |
Velocity |
94.43
(.001) |
V1<V2<V3<V4 |
0.86 |
|
Segment |
97.71
(.001) |
a>b>c>d>e |
0.86 |
|
|
Velocity*Segment |
25.54
(.001) |
- |
0.62 |
|
|
Horizontal Acc. |
Velocity |
50.68 (.001) |
V1<V2<V3<V4 |
0.76 |
|
Segment |
126.06 (.001) |
a>b>c>d,e |
0.89 |
|
|
Velocity*Segment |
24.82 (.001) |
- |
0.61 |
|
|
3-axis Acc. |
Velocity |
91.68 (.001) |
V1<V2<V3<V4 |
0.85 |
|
Segment |
175.86 (.001) |
a>b>c>d>e |
0.92 |
|
|
Velocity*Segment |
36.20 (.001) |
- |
0.69 |
|
|
Note. *: significant at p<.05; V1: 2.5 m/s,
V2: 3.0 m/s, V3: 3.5 m/s, V4: 4.0 m/s; a: distal tibia, b: proximal tibia, c:
L5, d: sternum, e: head |
||||
3. 주파수 영역에서의 파워 스펙트럼 밀도 및 최대 주파수: 속도 및 신체 분절에 따른 분석
충격 주파수(10-20 Hz) 범위 내, 충격 가속도의 PSD와 최대 주파수는 속도와 신체 분절에 따라 유의한 차이가 나타났다(p<.05). 최대 주파수는 속도 증가에 따라 전체 분절에서 증가하는 경향을 보였으며, 특히 4.0 m/s에서 가장 높은 주파수 값이 나타났다. PSD 역시 속도 증가에 따라 전반적으로 증가하였으며, 먼쪽 정강뼈와 몸쪽 정강뼈에서 가장 높은 PSD 값이, 머리에서 가장 낮은 PSD 값이 나타났다. 모든 변수에서 속도와 분절에 대한 효과 크기는 η2 = .63-.79로 높게 나타났다(Table 4-6).
|
Axis |
Segment |
V1 |
V2 |
V3 |
V4 |
|
Vertical |
Distal tibia |
14.50±1.57 |
15.44±1.73 |
16.00±1.60 |
16.44±1.26 |
|
Proximal tibia |
13.64±0.97 |
14.81±1.66 |
15.52±1.81 |
15.73±1.57 |
|
|
L5 |
14.51±2.32 |
14.72±2.62 |
14.64±2.82 |
15.12±2.41 |
|
|
Sternum |
15.38±2.01 |
15.33±1.91 |
14.87±2.48 |
14.95±1.94 |
|
|
Head |
15.81±2.26 |
15.89±2.04 |
15.29±2.39 |
14.29±2.04 |
|
|
Horizontal |
Distal tibia |
14.41±2.26 |
14.08±2.31 |
13.73±1.91 |
13.46±0.76 |
|
Proximal tibia |
13.73±2.16 |
13.65±2.06 |
13.72±1.80 |
13.91±2.05 |
|
|
L5 |
15.74±2.44 |
15.36±2.58 |
15.08±2.75 |
14.92±2.30 |
|
|
Sternum |
13.84±1.80 |
12.92±1.72 |
12.85±1.50 |
13.09±1.28 |
|
|
Head |
12.56±0.77 |
12.30±1.49 |
11.83±1.16 |
12.42±1.20 |
|
|
3-axis |
Distal tibia |
15.71±1.58 |
14.38±2.78 |
12.28±1.94 |
12.29±0.92 |
|
Proximal tibia |
14.61±2.72 |
12.61±2.36 |
11.87±1.78 |
11.76±1.09 |
|
|
L5 |
13.49±2.01 |
13.24±2.16 |
13.08±2.27 |
13.66±2.01 |
|
|
Sternum |
15.60±2.12 |
15.34±1.77 |
15.10±2.27 |
14.67±1.78 |
|
|
Head |
15.34±2.37 |
15.28±2.26 |
14.62±2.34 |
14.12±1.89 |
|
|
Note. V1: 2.5 m/s, V2: 3.0 m/s,
V3: 3.5 m/s, V4: 4.0 m/s |
|||||
|
Axis |
Segment |
V1 |
V2 |
V3 |
V4 |
95% CI |
95% CI |
|
Vertical |
Distal tibia |
0.034±0.017 |
0.045±0.023 |
0.074±0.039 |
0.130±0.061 |
0.054 |
0.088 |
|
Proximal tibia |
0.070±0.056 |
0.085±0.075 |
0.136±0.100 |
0.224±0.141 |
0.083 |
0.175 |
|
|
L5 |
0.012±0.010 |
0.015±0.011 |
0.018±0.012 |
0.023±0.015 |
0.011 |
0.023 |
|
|
Sternum |
0.006±0.003 |
0.006±0.004 |
0.009±0.009 |
0.010±0.005 |
0.006 |
0.010 |
|
|
Head |
0.003±0.002 |
0.004±0.002 |
0.004±0.002 |
0.005±0.003 |
0.003 |
0.005 |
|
|
95% CI |
0.017 |
0.021 |
0.034 |
0.059 |
|
|
|
|
95% CI |
0.032 |
0.041 |
0.062 |
0.098 |
|
|
|
|
Horizontal Acc. |
Distal tibia |
0.010±0.003 |
0.013±0.004 |
0.026±0.013 |
0.047±0.025 |
0.020 |
0.028 |
|
Proximal tibia |
0.011±0.006 |
0.012±0.006 |
0.016±0.010 |
0.027±0.014 |
0.013 |
0.021 |
|
|
L5 |
0.004±0.003 |
0.007±0.004 |
0.008±0.005 |
0.011±0.004 |
0.006 |
0.009 |
|
|
Sternum |
0.003±0.004 |
0.003±0.002 |
0.005±0.004 |
0.004±0.002 |
0.003 |
0.004 |
|
|
Head |
0.001±0.001 |
0.001±0.001 |
0.001±0.001 |
0.001±0.001 |
0.001 |
0.001 |
|
|
95% CI |
0.005 |
0.006 |
0.009 |
0.015 |
|
|
|
|
95% CI |
0.007 |
0.008 |
0.013 |
0.022 |
|
|
|
|
3-axis |
Distal tibia |
0.011±0.005 |
0.019±0.012 |
0.040±0.022 |
0.061±0.023 |
0.026 |
0.039 |
|
Proximal tibia |
0.009±0.007 |
0.018±0.014 |
0.040±0.025 |
0.069±0.036 |
0.025 |
0.043 |
|
|
L5 |
0.010±0.009 |
0.013±0.011 |
0.014±0.009 |
0.021±0.013 |
0.010 |
0.019 |
|
|
Sternum |
0.006±0.004 |
0.006±0.004 |
0.010±0.012 |
0.010±0.005 |
0.005 |
0.010 |
|
|
Head |
0.003±0.002 |
0.004±0.002 |
0.005±0.003 |
0.005±0.003 |
0.003 |
0.005 |
|
|
95% CI |
0.006 |
0.009 |
0.016 |
0.028 |
|
|
|
|
95% CI |
0.009 |
0.015 |
0.027 |
0.039 |
|
|
|
|
Note.
V1: 2.5 m/s, V2: 3.0 m/s, V3: 3.5 m/s, V4: 4.0 m/s; 95% CI: 95% confidence
interval |
|||||||
|
Axis |
|
F (p) |
Post-hoc |
Effect size (η2) |
|
Vertical |
Velocity |
59.493 (.001) |
V1<V2<V3<V4 |
0.788 |
|
Segment |
30.585 (.001) |
a,b>c>e,
a,b>d |
0.657 |
|
|
Velocity*Segment |
33.649 (.001) |
- |
0.678 |
|
|
Horizontal resultant Acc. |
Velocity |
37.281 (.001) |
V1<V2<V3<V4 |
0.7 |
|
Segment |
64.526 (.001) |
b>a>c>d>e |
0.801 |
|
|
Velocity*Segment |
17.910 (.001) |
- |
0.528 |
|
|
3-axis Acc. |
Velocity |
60.085 (.001) |
V1<V2<V3<V4 |
0.79 |
|
Segment |
36.318 (.001) |
a,b>c>e,n
a,b>d |
0.694 |
|
|
Velocity*Segment |
27.320 (.001) |
- |
0.631 |
|
|
Note. *: significant at p<.05; V1: 2.5 m/s, V2: 3.0 m/s,
V3: 3.5 m/s, V4: 4.0 m/s; a: distal tibia, b: proximal tibia, c: L5, d:
sternum, e: head |
||||
본 연구는 달리기 속도(2.5 m/s, 3.0 m/s, 3.5 m/s, 4.0 m/s)에 따른 수직 지면반력과 신체 부위별 충격 가속도 특성을 분석하기 위해 수행되었다. 분석을 위해 수직 지면반력의 충격력과 능동력을 분리하여 산출하였으며, 신체 각 분절의 시간 영역 충격 가속도와 주파수 영역 특성(최대 주파수와 PSD)을 비교 및 분석하였다.
우선 수직 지면반력 결과를 살펴보면, Shorten과 Mientjes (2011)은 지면반력의 고주파 성분이 착지 직후 짧은 시간 내에 발생하는 충격력의 특성과 시점을 효과적으로 반영하며, 저주파 성분은 체중 지지 및 추진 단계에서 발생하는 신체 움직임에 의한 에너지 전달을 나타낸다고 보고하였다. 이에 본 연구는 선행연구를 바탕으로, 수직 지면반력 자료를 10 Hz를 기준으로 저역통과 및 고역통과 필터링하여 충격 성분과 능동 성분을 분리하고, 각각의 최대 피크를 능동력과 충격력으로 정의하였다. 그 결과, 달리기 속도가 증가할수록 최대 충격력과 최대 능동력은 모두 통계적으로 유의하게 증가하였다. 특히 4.0 m/s의 빠른 속도에서는 약 79%의 충격력과 7%의 능동력 증가가 관찰되었으며, 이와 같이 속도 증가에 따른 충격력 및 능동력 증가는 선행연구의 결과와도 일치한다(De Wit, De Clercq & Aerts, 2000; Nigg, Bahlsen, Luethi & Stokes, 1987; Lee, Kang & Park, 2024). 이러한 경향은 빠른 속도 달리기 시, 발의 지면 접촉 시간 감소, 스텝 길이 증가, 하지 관절 각도 증가에 의해 착지 충돌 속도가 증가하기 때문에(Breine, Malcolm, Frederick & De Clercq, 2014; Brughelli, Cronin & Chaouachi, 2011; Fukuchi, Fukuchi & Duarte, 2017; Orendurff et al., 2018) 발생하는 기계적 반작용력 증대에 기인한 것으로 사료되며, 속도 증가에 따라 하지 분절에서의 충격 강도는 물론, 상체로의 충격 전달 양상에도 영향을 미칠 수 있을 것으로 사료된다.
다음으로, 달리기 속도에 따른 신체 각 분절의 충격 가속도를 시간 영역에서 분석한 결과, 모든 분절(먼쪽 정강뼈, 몸쪽 정강뼈, 5번째 허리뼈, 앞 가슴뼈, 머리)의 수직 가속도, 수평 합성 가속도, 3축 합성 가속도는 모두 유의하게 증가하였다. 세 성분 중 3축 합성 가속도가 가장 큰 진폭을 나타냈으며, 이는 다양한 방향의 충격 성분이 벡터 형태로 결합되었기 때문으로 해석된다. 특히 수직 가속도는 착지 시 충격의 주요 전달 방향과 일치하여 개별 축 중에서는 가장 큰 값이 관찰된 반면, 수평 합성 가속도는 착지 유형이나 측방 흔들림 등 복합적 요인의 영향을 받아 상대적으로 작은 진폭과 높은 변동성이 나타난 것으로 판단된다. 속도 증가에 따른 3축 합성 가속도의 변화율을 보면, 2.5 m/s에서 4.0 m/s로 속도가 증가함에 따라 먼쪽 정강뼈는 약 85%, 몸쪽 정강뼈는 약 71% 상승하였다. 이에 반해 5번째 허리뼈와 앞 가슴뼈, 머리에서는 각각 41%, 19%, 15%로 상대적으로 완만하게 증가되는 양상을 보였다. 이러한 결과는 달리기 속도가 증가함에 따라 지면 충격의 절대량은 증가하지만, 충격이 하위 분절에서 상위 분절로 전달되는 과정에서 신체의 굽힘-폄 동작과 신체 내 연조직 등 체내 구조물들이 충격을 효과적으로 흡수 및 감쇠시킨다는 것을 시사한다(Bertelsen et al., 2017; Kulmala et al., 2013a; Laughton, Davis & Hamill, 2003; Voloshin & Wosk, 1982). 또한, 속도에 따른 각 분절 간 충격 가속도 감소율을 비교해 보면, 2.5 m/s에서의 감소율(먼쪽 정강뼈-몸쪽 정강뼈: -20.26%, 몸쪽 정강뼈-5번째 허리뼈: -26.56%, 5번째 허리뼈-앞 가슴뼈: -20.76%, 앞 가슴뼈-머리: -28.73%)보다 4.0 m/s에서의 감소율(-26.48%, -39.29%, -33.07%, -31.44%)이 더 크게 나타났다. 이는 빠른 달리기일수록 지면 접촉 시간은 짧아지고, 착지 충돌 속도가 증가하면서(Breine et al., 2014; Brughelli et al., 2011; Lee et al., 2024), 전체적인 하지 관절 강성이 증가하기 때문으로 해석된다(Arampatzis, Brüggemann & Metzler, 1999; Brughelli & Cronin, 2008). 즉, 2.5 m/s 달리기에서는 상대적으로 작은 충격 에너지를 충분한 시간 동안 관절 가동범위를 움직여 점진적으로 흡수하는 반면, 4.0 m/s 달리기에서는 순간적으로 큰 충격 에너지를 흡수하여 근육-건 단위의 탄성 요소를 일시적으로 저장하였다가 방출한다(Butler, Crowell III & Davis, 2003; Cunningham, Hunter, Seeley & Feland, 2013; Farley & Gonzalez, 1996). 이러한 메커니즘은 달리기 효율과 속도를 향상시키지만, 더 큰 충격력이 신체에 전달되어 과사용 부상의 위험을 높일 수 있다(Butler et al., 2003; Hreljac, 2004). 결론적으로, 시간 영역에서의 충격 가속도 분석은 속도 증가에 따른 인체 충격의 분포 양상과 생체 감쇠 특성을 정량적으로 파악할 수 있는 유효한 도구이며, 특히 속도에 따라 특정 분절에 과도한 충격이 집중되는 경향은 향후 RRI 예방 및 트레이닝 전략 수립에 중요한 기초자료로 활용될 수 있을 것으로 사료된다.
마지막으로 주파수 영역의 분석 결과를 살펴보면, 수직 가속도, 수평 합성 가속도, 3축 합성 가속도 모두에서 속도 증가에 따라 PSD는 유의하게 증가한 반면, 최대 주파수는 대부분의 분절에서 일정한 범위(약 13-16 Hz)를 유지하였다(Lucas-Cuevas et al., 2017). 특히 수직 가속도의 경우를 살펴보면, 달리기 속도 2.5 m/s에서 4.0 m/s로 속도가 증가함에 따라 먼쪽 정강뼈는 약 3.8배, 몸쪽 정강뼈는 약 3.2배로 하지 분절에서 뚜렷한 PSD 증가폭을 보인 반면, 상체 분절에서는 5번째 허리뼈가 약 1.9배, 앞 가슴뼈가 약 1.7배, 머리가 약 1.6배로 증가폭이 상대적으로 제한적이었으며, 각 분절 간 충격 감소율은 2.5 m/s에서 먼쪽 정강뼈-몸쪽 정강뼈 105.88%, 몸쪽 정강뼈-5번째 허리뼈 -82.86%, 5번째 허리뼈-앞 가슴뼈 -50%, 앞 가슴뼈-머리 -50%, 4.0 m/s에서는 각각 72.31%, -89.73%, -56.52%, -50%로 나타났다. 이와 같은 결과는 본 연구에서 설정한 두 가지 연구 가설을 지지하며, 달리기 속도가 증가함에 따라 인체가 받는 충격도 증가한다는 선행연구와도 일치한다(Breine et al., 2014; Brughelli et al., 2011; Lee et al., 2024). 또한, 시간 영역 분석과 마찬가지로 속도가 증가함에 따라 하지 분절에서는 충격이 급격히 증가하나, 몸통과 머리로 갈수록 점진적으로 감쇠되는 생체역학적 충격 흡수 메커니즘을 뒷받침한다(Bertelsen et al., 2017; Kulmala et al., 2013a; Laughton et al., 2003; Voloshin & Wosk, 1982).
한편, 주파수 영역 결과에서 주목할 점은 수직 가속도 성분의 몸쪽 정강뼈 PSD가 먼쪽 정강뼈의 PSD에 비해 더 높게 나타났다는 것이다. 이러한 경향은 Lucas-Cuevas 등 (2017)이 제시한 고주파 PSD 결과와도 일치하지만, 지면 접촉 부위에서 큰 충격이 시작되어 상방으로 올라갈수록 충격이 감쇠된다는 시간 영역의 분석 결과와는 다소 상반된다. 이는 충격이 하위 분절에서 상위 분절로 단순히 감쇠되는 선형적 흐름이 아니라, 신체 각 부위의 구조적 특성이나 고유 진동 특성(natural frequency), 착지 전략 등 복합적인 생체역학적 요인에 따라 특정 부위에서 국소적인 진동 에너지가 증폭될 수 있음을 시사한다. Lucas-Cuevas 등 (2017)은 연부 조직의 감쇠 특성이 몸쪽 정강뼈 부위에서 더 강하게 작용하여 저주파수 성분에서는 진폭이 감소하는 반면, 고주파수 성분은 이러한 감쇠 효과의 영향을 덜 받기 때문에 오히려 몸쪽 정강뼈 부위에서 더 높은 PSD가 관찰될 수 있다고 보고한 바 있다. 이는 몸쪽 정강뼈에서의 고주파 PSD 증가가 단순한 해부학적 위치뿐 아니라, 해당 부위의 진동 전달 및 감쇠 특성과 연관되어 있을 가능성을 보여준다. 또한, 고주파는 짧은 시간 내 반복적으로 진동하거나 변화하는 신호로, 단시간 내 충격 반응이나 미세한 진동 특성을 민감하게 반영하는 특성이 있어(Gruber et al., 2014; Winslow & Shorten, 1989), 이러한 고주파 에너지가 몸쪽 정강뼈에서 효과적으로 감쇠되지 않고 잔존하게 될 경우, 해당 부위나 인접 관절인 무릎에 과도한 기계적 부하가 가해질 수 있으며 무릎 상해율을 증가시킬 수 있다(Shorten & Winslow, 1992).
달리기 상해 선행연구들을 살펴보면, 후족 착지 달리기 시, 무릎 관절에 전달되는 충격부하가 크며, 이에 무릎 관련 상해 발생률이 높게 보고되고 있다(Goss & Gross, 2012; Kulmala Avela, Pasanen & Parkkari, 2013b; Lopes et al., 2012). 따라서 본 연구의 결과는 고주파 PSD가 몸쪽 정강뼈에서 크게 나타난 현상이 단순한 해부학적 위치나 진동 전달 경로 외에도, 착지 유형 및 상체로의 감쇠 한계와 연계된 생체역학적 부하가 반영된 결과일 가능성도 보여준다. 향후 연구에서는 착지 유형(후족 착지, 중족 착지, 전족 착지)에 따른 고주파 성분 비교 및 분석을 통해, 상해 예방 관점에서 보다 정교한 착지 전략 수립이 필요할 것이다.
한편, 최대 주파수는 전반적으로 14-16 Hz 범위에서 유지되었으며, 속도 증가에 따라 일부 분절에서 소폭 상승하는 경향은 관찰되었으나 통계적으로 뚜렷한 변화는 나타나지 않았다. 이러한 경향은 Lucas-Cuevas 등 (2017)의 연구에서 제시한 2.22-3.33 m/s 구간의 최대 주파수 값(13.87-14.40 Hz)과도 유사하며, 속도의 변화가 충격 에너지의 크기(PSD)에는 영향을 주지만, 충격의 발생 주기나 파형 빈도(peak frequency)에는 상대적으로 제한적인 영향을 미친다는 점을 시사한다. 결과적으로, 주파수 영역에서의 충격 가속도 분석은 단순한 최대 진폭 비교를 넘어, 속도 변화에 따라 충격이 어느 주파수 대역에서 집중되고, 신체 내에서 어떻게 감쇠 또는 변형되는지를 정량적으로 파악할 수 있는 유효한 분석 도구이다. 특히 고속 달리기 시 하지에 집중되는 고주파 충격 특성은 RRI 예방, 착지 전략 수립, 신발 구조 설계 등 다양한 실무적 활용 가능성을 제시한다.
본 연구는 달리기 속도 증가가 인체에 전달되는 충격의 특성, 특히 주파수 영역에서의 충격 가속도 특성에 어떠한 영향을 미치는지를 분석하였다. 주요 결과로는 다음과 같은 사실이 확인되었다. 첫째, 달리기 속도가 증가함에 따라 수직 지면반력의 충격력과 능동력 모두 유의하게 증가하였다. 둘째, 시간 영역에서는 인체 모든 분절에서 수직 가속도, 수평 합성 가속도, 3축 합성 가속도가 모두 유의하게 증가하였으며, 하지에서 상체로 갈수록 충격이 점진적으로 감쇠되는 경향을 보였다. 셋째, 주파수 영역에서는 속도 증가에 따라 PSD가 현저히 증가하였으며, 특히 하지 분절에서 뚜렷한 증가가 나타났지만, 최대 주파수는 전반적으로 일정한 범위(약 13-16 Hz) 내에서 유지되었다.
이러한 결과는 달리기 시 속도 증가가 인체에 전달되는 기계적 부하의 크기뿐 아니라, 고주파 충격 에너지의 집중도를 증폭시킴을 시사한다. 특히 몸쪽 정강뼈에서 관찰된 높은 PSD 값은 해당 부위가 고주파 진동에 취약한 구조적 특성을 가질 가능성을 제시하며, 이는 무릎 부위의 과사용 부상 위험과도 밀접하게 연관될 수 있다. 본 연구는 주파수 영역에서의 충격 특성을 정량적으로 규명함으로써 기존의 시간 영역 기반 분석의 한계를 보완하고, 보다 정교한 부상 예방 전략 및 착지 방식 개선, 기능성 신발 설계 등에 실질적인 시사점을 제공한다.
그러나 본 연구는 특정 착지 유형(후족 착지)과 제한된 속도 조건(2.5-4.0 m/s), 실험실 환경(트레드밀 달리기)이라는 점에서 일반화에 한계가 있으며, 신체 내 연부 조직의 해부학적 특성과 진동 특성이 개입된 충격 감쇠 메커니즘에 대한 직접적인 규명이 부족하였다. 따라서 향후 연구에서는 다양한 착지 유형과 보행 형태, 연령 또는 성별에 따른 차이를 포함한 확장된 조건에서의 분석이 필요하며, 충격 진동이 연부 조직에 미치는 생리적 영향을 함께 고려한 다학제적 접근이 요구된다.
References
1. Almeida, M. O., Davis, I. S. & Lopes, A. D. (2015). Biomechanical differences of foot-strike patterns during running: a sys- tematic review with meta-analysis. Journal of Orthopaedic & Sports Physical Therapy, 45(10), 738-755.
Google Scholar
2. Arampatzis, A., Brüggemann, G. P. & Metzler, V. (1999). The effect of speed on leg stiffness and joint kinetics in human running. Journal of Biomechanics, 32(12), 1349-1353.
Google Scholar
3. Arendse, R. E., Noakes, T. D., Azevedo, L. B., Romanov, N., Schwellnus, M. P. & Fletcher, G. (2004). Reduced eccentric loading of the knee with the pose running method. Medicine & Science in Sports & Exercise, 36(2), 272-277.
Google Scholar
4. Bertelsen, M. L., Hulme, A., Petersen, J., Brund, R. K., Sørensen, H., Finch, C. F., Parner, E. T. & Nielsen, R. O. (2017). A framework for the etiology of running related injuries. Scandinavian Journal of Medicine & Science in Sports, 27(11), 1170-1180.
Google Scholar
5. Blackmore, T., Willy, R. W. & Creaby, M. W. (2016). The high frequency component of the vertical ground reaction force is a valid surrogate measure of the impact peak. Journal of Biomechanics, 49(3), 479-483.
Google Scholar
6. Breine, B., Malcolm, P., Frederick, E. C. & De Clercq, D. (2014). Relationship between running speed and initial foot con- tact patterns. Medicine and Science in Sports and Exercise, 46(8), 1595-1603.
Google Scholar
7. Breine, B., Malcolm, P., Van Caekenberghe, I., Fiers, P., Frederick, E. C. & De Clercq, D. (2017). Initial foot contact and related kinematics affect impact loading rate in running. Journal of Sports Sciences, 35(15), 1556-1564.
Google Scholar
8. Brughelli, M. & Cronin, J. (2008). Influence of running velocity on vertical, leg and joint stiffness: Modelling and recom- mendations for future research. Sports Medicine, 38, 647-657.
Google Scholar
9. Brughelli, M., Cronin, J. & Chaouachi, A. (2011). Effects of running velocity on running kinetics and kinematics. The Journal of Strength & Conditioning Research, 25(4), 933-939.
Google Scholar
10. Butler, R. J., Crowell III, H. P. & Davis, I. M. (2003). Lower extremity stiffness: implications for performance and injury. Clinical Biomechanics, 18(6), 511-517.
Google Scholar
11. Castillo, E. R. & Lieberman, D. E. (2018). Shock attenuation in the human lumbar spine during walking and running. Journal of Experimental Biology, 221(9), jeb177949.
Google Scholar
12. Cunningham, R., Hunter, I., Seeley, M. K. & Feland, B. (2013). Variations in running technique between female sprinters, middle, and distance runners. International Journal of Exercise Science, 6(1), 43-51.
Google Scholar
13. De Wit, B., De Clercq, D. & Aerts, P. (2000). Biomechanical analysis of the stance phase during barefoot and shod running. Journal of Biomechanics, 33(269), 278.
Google Scholar
14. Farley, C. T. & Gonzalez, O. (1996). Leg stiffness and stride frequency in human running. Journal of Biomechanics, 29(2), 181-186.
Google Scholar
15. Fukuchi, R. K., Fukuchi, C. A. & Duarte, M. (2017). A public dataset of running biomechanics and the effects of running speed on lower extremity kinematics and kinetics. Peer J, 5, e3298.
Google Scholar
16. Giandolini, M., Horvais, N., Rossi, J., Millet, G. Y., Samozino, P. & Morin, J. B. (2016). Foot strike pattern differently affects the axial and transverse components of shock acceler- ation and attenuation in downhill trail running. Journal of Biomechanics, 49(9), 1765-1771.
Google Scholar
17. Glauberman, M. D. & Cavanagh, P. R. (2014). Rearfoot strikers have smaller resultant tibial accelerations at foot contact than non-rearfoot strikers. Journal of Foot and Ankle Research, 17(1), 1-2.
Google Scholar
18. Goss, D. L. & Gross, M. T. (2012). A review of mechanics and injury trends among various running styles. US Army Medical Department Journal, 62-71.
Google Scholar
19. Gruber, A. H., Boyer, K. A., Derrick, T. R. & Hamill, J. (2014). Impact shock frequency components and attenuation in rearfoot and forefoot running. Journal of Sport and Health Science, 3(2), 113-121.
Google Scholar
20. Hamill, J., Derrick, T. R. & Holt, K. G. (1995). Shock attenuation and stride frequency during running. Human Movement Science, 14(1), 45-60.
Google Scholar
21. Hennig, E. M. & Lafortune, M. A. (1991). Relationships between ground reaction force and tibial bone acceleration param- eters. Journal of Applied Biomechanics, 7(3), 303-309.
Google Scholar
22. Hollis, C. R., Koldenhoven, R. M., Resch, J. E. & Hertel, J. (2019). Running biomechanics as measured by wearable sensors: effects of speed and surface. Sports Biomechanics, 20(5), 521-531.
Google Scholar
23. Hreljac, A. (2004). Impact and overuse injuries in runners. Medicine & Science in Sports & Exercise, 36(5), 845-849.
Google Scholar
24. Hreljac, A. L. A. N., Marshall, R. N. & Hume, P. A. (2000). Evaluation of lower extremity overuse injury potential in runners. Medicine & Science in Sports & Exercise, 32(9), 1635-1641.
Google Scholar
25. Kulmala, J. P., Avela, J., Pasanen, K. & Parkkari, J. (2013a). Effects of striking strategy on lower extremity loading during running. British Journal of Sports Medicine, 47(10), e3.
Google Scholar
26. Kulmala, J. P., Avela, J., Pasanen, K. & Parkkari, J. (2013b). Fore- foot strikers exhibit lower running-induced knee loading than rearfoot strikers. Medicine and Science in Sports and Exercise, 45(12), 2306-2313.
Google Scholar
27. Kyröläinen, H., Komi, P. V. & Belli, A. (1999). Changes in muscle activity patterns and kinetics with increasing running speed. Journal of Strength & Conditioning Research, 13(4), 400-406.
Google Scholar
28. Laughton, C. A., Davis, I. M. & Hamill, J. (2003). Effect of strike pattern and orthotic intervention on tibial shock during running. Journal of Applied Biomechanics, 19(2), 153-168.
Google Scholar
29. Lee, Y. S., Kang, J. W. & Park, S. K. (2024). Effects of running speed on body impact acceleration and biomechanical variables. Korean Journal of Applied Biomechanics, 34(2), 81-92.
Google Scholar
30. Lieberman, D. E., Venkadesan, M., Werbel, W. A., Daoud, A. I., D'andrea, S., Davis, I. S., Mang'Eni, R. O. & Pitsiladis, Y. (2010). Foot strike patterns and collision forces in habit- ually barefoot versus shod runners. Nature, 463(7280), 531-535.
Google Scholar
31. Lopes, A. D., Hespanhol, L. C., Yeung, S. S. & Costa, L. O. P. (2012). What are the main running-related musculoskeletal injuries?. Sports Medicine, 42(10), 891-905.
Google Scholar
32. Lucas-Cuevas, A. G., Encarnación-Martínez, A., Camacho-García, A., Llana-Belloch, S. & Pérez-Soriano, P. (2017). The location of the tibial accelerometer does influence impact acceleration parameters during running. Journal of Sports Sciences, 35(17), 1734-1738.
Google Scholar
33. MacLellan, G. E. & Vyvyan, B. (1981). Management of pain beneath the heel and Achilles tendonitis with visco-elastic heel inserts. British Journal of Sports Medicine, 15(2), 117-121.
Google Scholar
34. Malisoux, L., Gette, P., Backes, A., Delattre, N., Cabri, J. & Theisen, D. (2021). Relevance of frequency-domain analyses to relate shoe cushioning, ground impact forces and running injury risk: A secondary analysis of a randomized trial with 800+ recreational runners. Frontiers in Sports and Active Living, 3, 744658.
Google Scholar
35. Malisoux, L., Nielsen, R. O., Urhausen, A. & Theisen, D. (2015). A step towards understanding the mechanisms of running-related injuries. Journal of Science and Medicine in Sport, 18(5), 523-528.
Google Scholar
36. Mercer, J. A., Bates, B. T., Dufek, J. S. & Hreljac, A. (2003). Char- acteristics of shock attenuation during fatigued running. Journal of Sports Science, 21(11), 911-919.
Google Scholar
37. Nielsen, R. O., Buist, I., Sørensen, H., Lind, M. & Rasmussen, S. (2012). Training errors and running related injuries: a systematic review. International Journal of Sports Physical Therapy, 7(1), 58.
Google Scholar
38. Nigg, B. M., Bahlsen, H. A., Luethi, S. M. & Stokes, S. (1987). The influence of running velocity and midsole hardness on external impact forces in heel-toe running. Journal of Biomechanics, 20(10), 951-959.
Google Scholar
39. Norris, M., Anderson, R. & Kenny, I. C. (2014). Method analysis of accelerometers and gyroscopes in running gait: a sys- tematic review. Proceedings of the institution of mechanical engineers. Journal of Sports Engineering and Technology, 228, 3-15.
Google Scholar
40. Orendurff, M. S., Kobayashi, T., Tulchin-Francis, K., Tullock, A. M. H., Villarosa, C., Chan, C., Kraus. E. & Strike, S. (2018). A little bit faster: Lower extremity joint kinematics and kinetics as recreational runners achieve faster speeds. Journal of Biomechanics, 71, 167-175.
Google Scholar
41. Park, S. K., Stefanyshyn, D., Ryu, S., Gil, H., Lee, Y. S., Kim, J. & Ryu, J. (2022). Comparisons of age-related changes in impact characteristics between healthy older and younger runners. International Journal of Precision Engineering and Manufacturing, 23(12), 1465-1476.
Google Scholar
42. Reenalda, J., Maartens, E., Buurke, J. H. & Gruber, A. H. (2019). Kinematics and shock attenuation during a prolonged run on the athletic track as measured with inertial magnetic measurement units. Gait & Posture, 68, 155-160.
Google Scholar
43. Ryu, J. S. (2020). Running speed on the magnitude of impact shock attenuation during ground contact. Korean Journal of Applied Biomechanics, 30(3), 197-204.
Google Scholar
44. Ryu, J. S., Yoon, S. H. & Park, S. K. (2016). Relationship between attenuation of impact shock at high frequency and flexion-extension of the lower extremity joints during downhill running. Korean Journal of Applied Biomechanics, 26(2), 167-174.
Google Scholar
45. Ryu, S., Lee, Y. S. & Park, S. K. (2021). Impact signal differences dependent on the position of accelerometer attachment and the correlation with the ground reaction force during running. International Journal of Precision Engineering and Manufacturing, 22(10), 1791-1798.
Google Scholar
46. Ryu, J. S. & Yoon, H. J. (2005). Magnitudes of impact force, impact shock, and shock attenuation of the elderly during the running. Korean Journal of Physical Education, 44(2), 327-340.
47. Same, M. H., Gandubert, G., Gleeton, G., Ivanov, P. & Landry Jr, R. (2020). Simplified welch algorithm for spectrum moni- toring. Applied Sciences, 11(1), 86.
Google Scholar
48. Shorten, M. R. & Winslow, D. S. (1992). Spectral analysis of impact shock during running. Journal of Applied Bio- mechanics, 8(4), 288-304.
Google Scholar
49. Shorten, M. & Mientjes, M. I. (2011). The 'heel impact' force peak during running is neither 'heel' nor 'impact' and does not quantify shoe cushioning effects. Footwear Science, 3(1), 41-58.
Google Scholar
50. Van Gent, R. N., Siem, D., van Middelkoop, M., Van Os, A. G., Bierma-Zeinstra, S. M. A. & Koes, B. W. (2007). Incidence and determinants of lower extremity running injuries in long distance runners: a systematic review. British Journal of Sports Medicine, 41(8), 469-480.
Google Scholar
51. Voloshin, A. & Wosk, J. (1982). An in vivo study of low back pain and shock absorption in the human locomotor system. Journal of Biomechanics, 15(1), 21-27.
Google Scholar
52. Welch, P. (2003). The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans- actions on Audio and Electroacoustics, 15(2), 70-73.
Google Scholar
53. Winslow, D. S. & Shorten, M. R. (1989). Spectral analysis of impact shock during running. Journal of Biomechanics, 22(10), 1099.